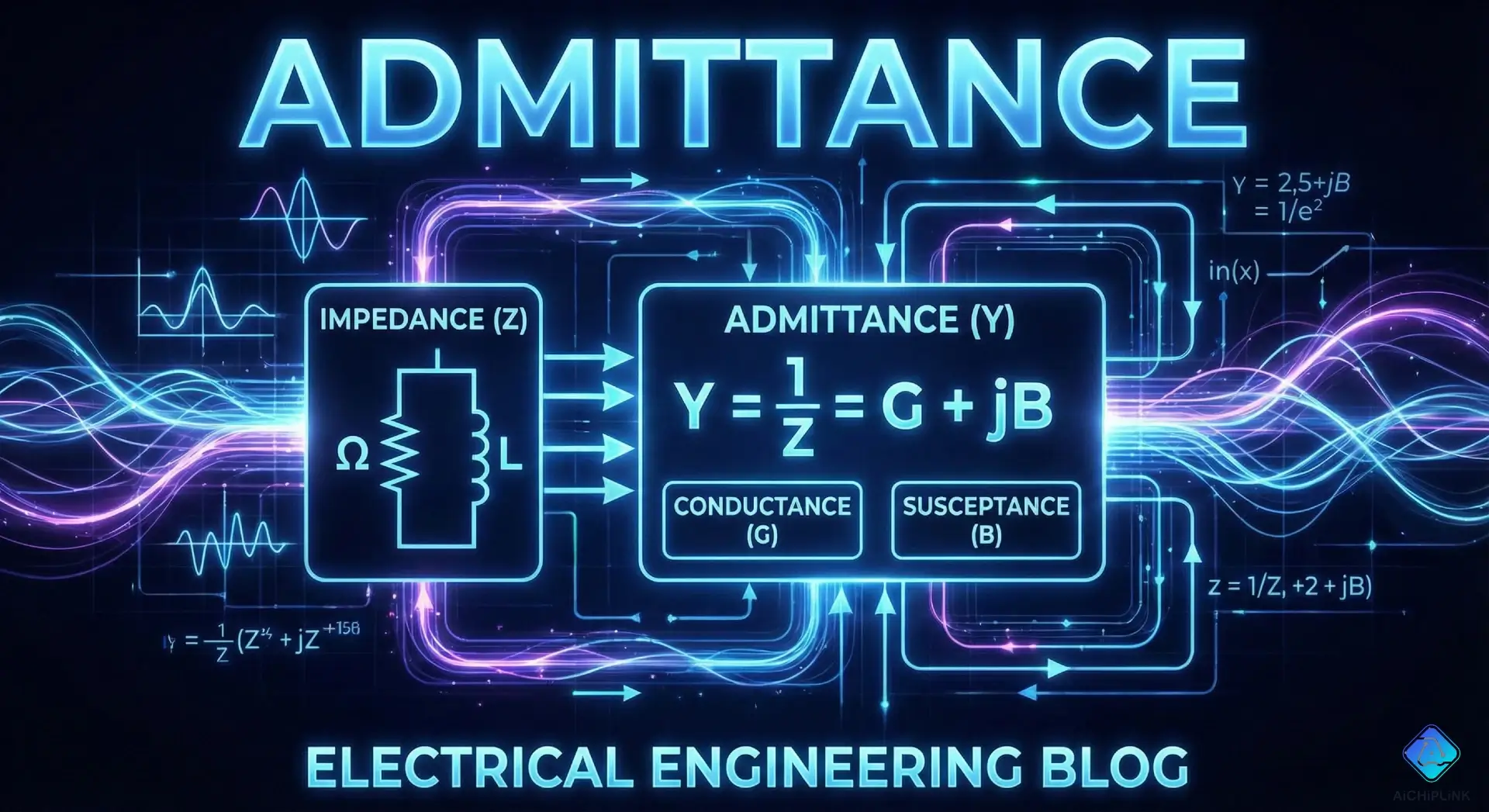
Admittance is a fundamental concept in electrical engineering, representing how easily a circuit or device allows alternating current (AC) to flow. It is the reciprocal of Impedance ($Z$). While Impedance measures opposition to current, Admittance measures the "allowance" of current.
Key Takeaways
- Definition: Admittance ($Y$) is the inverse of Impedance ($Z$). $Y = \frac{1}{Z}$.
- Unit: The SI unit is the Siemens (S). Historically, it was known as the "Mho" ($\mho$).
- Components: Admittance is a complex number consisting of a real part, Conductance ($G$), and an imaginary part, Susceptance ($B$). Formula: $Y = G + jB$.
- Primary Use: Admittance simplifies calculations in parallel AC circuits, where total admittance is simply the sum of individual admittances ($Y_T = Y_1 + Y_2 + ...$).
- Relationship: High Admittance = Low Impedance = High Current Flow.
Introduction
In DC circuits, we talk about Resistance ($R$). In AC circuits, we expand this to Impedance ($Z$), which accounts for frequency-dependent opposition to current.
But what if, instead of asking "How much does this circuit resist flow?", we asked "How easily does this circuit allow flow?"
That is Admittance.
Admittance is the mirror image of Impedance. While it might seem redundant at first, understanding Admittance allows engineers to solve complex parallel circuit problems with simple addition rather than messy fractions.
What is Admittance? The Formula
Mathematically, Admittance (symbolized as $Y$) is defined as the reciprocal of Impedance ($Z$).
$$Y = \frac{1}{Z}$$
Since Impedance is a complex number ($Z = R + jX$), Admittance is also a complex number composed of two parts:
$$Y = G + jB$$
Where:
- $Y$ = Admittance (measured in Siemens)
- $G$ = Conductance (The real part)
- $B$ = Susceptance (The imaginary part)
- $j$ = The imaginary unit ($\sqrt{-1}$)
The Components: Conductance and Susceptance
Just as Impedance is made of Resistance and Reactance, Admittance is made of Conductance and Susceptance.
1. Conductance ($G$)
Conductance represents the resistive component's ability to conduct current.
- Ideally: In a purely resistive DC circuit, Conductance is simply the reciprocal of Resistance ($G = \frac{1}{R}$).
- In AC: It is the real part of the complex admittance.
2. Susceptance ($B$)
Susceptance represents the ease with which current passes through a reactive component (Inductor or Capacitor).
- Inductive Susceptance ($B_L$): The inverse of Inductive Reactance.
- Capacitive Susceptance ($B_C$): The inverse of Capacitive Reactance.
Note on Signs: When you invert Impedance ($Z = R + jX$), the sign of the imaginary part flips. Therefore, while Inductive Reactance is positive, Inductive Susceptance is negative.
Units of Measurement
The SI unit for Admittance, Conductance, and Susceptance is the Siemens, symbolized by the capital letter S.
- Historical Fun Fact: Before the Siemens was adopted, the unit was called the Mho (which is "Ohm" spelled backward). The symbol for the Mho was an upside-down Omega ($\mho$). You may still see this in very old textbooks.
Why Use Admittance? (Series vs. Parallel)
This is the most important section for practical application. Why bother converting $Z$ to $Y$?
The Short Answer: Math is easier.
In Series Circuits: Use Impedance ($Z$)
When components are in series, you simply add their impedances: $$Z_{Total} = Z_1 + Z_2 + Z_3$$
In Parallel Circuits: Use Admittance ($Y$)
If you try to calculate total impedance for parallel components, the formula is messy: $$\frac{1}{Z_{Total}} = \frac{1}{Z_1} + \frac{1}{Z_2} + \frac{1}{Z_3}$$
However, if you convert those impedances to Admittance, the formula becomes a simple addition: $$Y_{Total} = Y_1 + Y_2 + Y_3$$
Once you sum the admittances, you can simply invert the result ($Z_T = \frac{1}{Y_T}$) to get the final impedance if needed. This makes Admittance the preferred tool for analyzing power distribution networks and parallel loads.
Conclusion
Admittance ($Y$) is more than just the mathematical inverse of Impedance; it is a powerful tool for simplifying AC circuit analysis. By breaking AC opposition into Conductance ($G$) and Susceptance ($B$), engineers can easily calculate the behavior of complex parallel networks.
Remember:
- Series Circuit? Think Impedance ($\Omega$).
- Parallel Circuit? Think Admittance ($S$).

Written by Jack Elliott from AIChipLink.
AIChipLink, one of the fastest-growing global independent electronic components distributors in the world, offers millions of products from thousands of manufacturers, and many of our in-stock parts is available to ship same day.
We mainly source and distribute integrated circuit (IC) products of brands such as Broadcom, Microchip, Texas Instruments, Infineon, NXP, Analog Devices, Qualcomm, Intel, etc., which are widely used in communication & network, telecom, industrial control, new energy and automotive electronics.
Empowered by AI, Linked to the Future. Get started on AIChipLink.com and submit your RFQ online today!
Frequently Asked Questions
What is the difference between Admittance and Impedance?
They are reciprocals of each other. Impedance ($Z$) measures how much a circuit **opposes** current flow, measured in Ohms. Admittance ($Y$) measures how easily a circuit **allows** current flow, measured in Siemens.
Can Admittance be zero?
Theoretically, yes. If a circuit has infinite Impedance (an open circuit), the Admittance is zero ($Y = 1/\infty = 0$). This means no current can flow.
Is Conductance ($G$) always just $1/R$?
Only in DC circuits or purely resistive AC circuits. In complex AC circuits containing reactance, converting $Z$ to $Y$ requires complex algebra, so $G$ is determined by both resistance ($R$) and reactance ($X$). Specifically: $G = \frac{R}{R^2 + X^2}$.
What is the symbol for Admittance?
The symbol is **$Y$**. The unit symbol is **$S$** (Siemens).
How do I convert Siemens back to Ohms?
Simply take the reciprocal. If you have a value of $0.05 S$, the Impedance in Ohms is $1 / 0.05 = 20 \Omega$.

.png&w=256&q=75)











